Algorithmic thinking is the must-have in the coding world, so I have been keeping the routine of algorithm practice every week, consolidating my knowledge of data structures on one hand, and improving my coding skills as well.
A difficult one happened to be stuck in my mind- Implement SkipList with Go, which took me quite a weekend. Below is the front-line report of how I finally got the hang of it.
First, from its concept. Wiki has explained it well.
a skip list is a probabilistic data structure that allows O(log n) search complexity as well as O(log n) insertion complexity within an ordered sequence of n elements.
In short, SkipList is a multi-layer-structured sort list for efficient queries. The bottom layer is an ordered LinkedList, and the upper layer extracts the bottom list and decomposes it into multiple lists that only contain certain index nodes.
To speed up queries, SkipList is adopted in many open-source libraries related to database storage. As far as I know, there are
Break down SkipList
SkipList algorithm
For an ordered LinkedList, the most efficient search algorithm is the binary search. For example
In this case, 3 steps to go to find 70.
- len(list) == 6, a[3] = 60, to find the middle variable in the list and compare.
- 60 < 70, the median value is less than 70, so search for the median value in the lower half of the list and compare, index = 3 + (6–3)/2 == 4.
- a[4] == 70, found.
The whole process is a repeat of locating the position, comparing, and getting closer to the ultimate index. And of course, the item may not exist anyway.
If you add an index level to the above list, the new two-level list will be
If we query 70 again, the steps will be finding 50 at the e2 level, and then finding 70, and the result found. It is also 3 steps though, the e2 level will accelerate queries at a nearly doubled speed when the list is with more elements and more lengthy. However, we cannot see its speed-up effect in this use case, which is too short.
The implementation of the SkipList is to superimpose level by level until there is only one element in the top level.
The SkipList is a transformation of the ordered linked list, adding a multi-layer index to the singly linked list, and applying the space-for-time strategy to improve query speed and quickly achieve range queries.
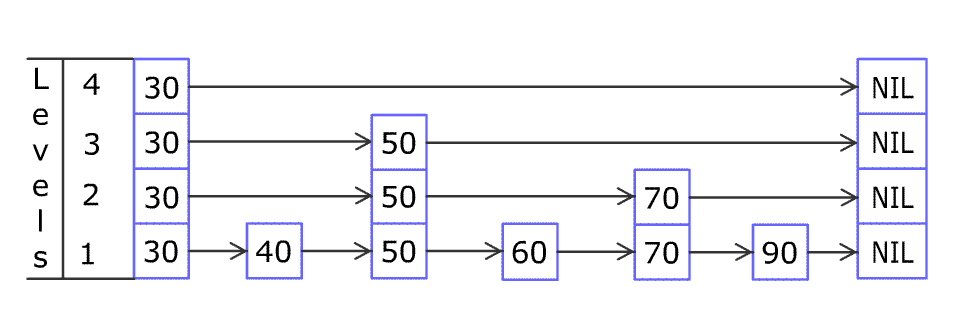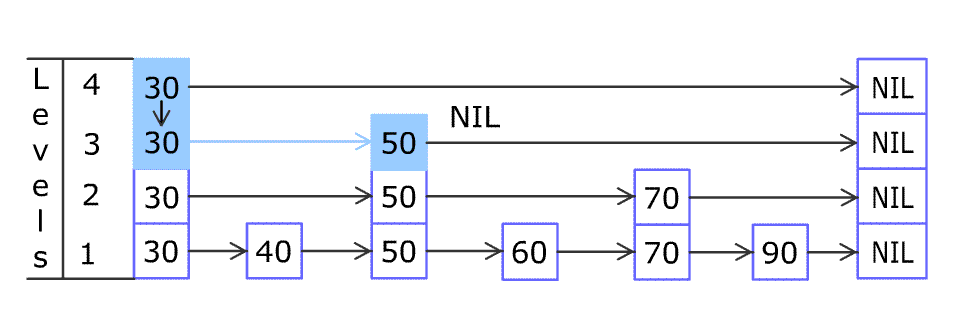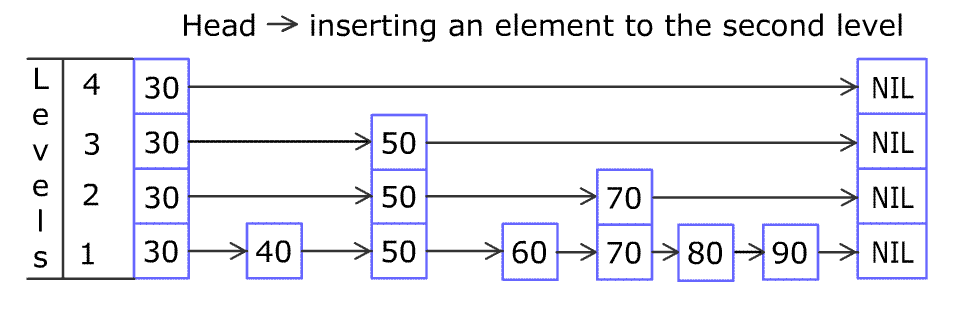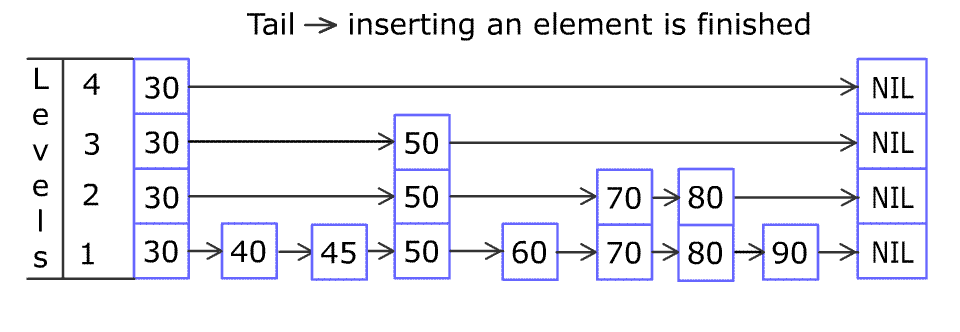
Inserting elements is the same. To ensure the order, you must find the right position. The following shows how to insert elements.
Time complexity
SkipList does improve the query speed, however, it is essentially a binary search. And the time complexity is still O(log n) according to the worst case, but the average has been boosted to O(n).
Implement SkipList
It’s no more a challenge to implement SkipList after understanding its structure.
Data structure
First, define the data structures required.
- Define a Node, which contains a multi-level index (level).
- Define the Level index, including the next Node.
- Then to the SkipList, which contains the head Node.
Set p as ½, and define the relatedNew method.
const (
MAX_L = 32
P = 0.5
)
type Node struct {
v int // value
ls []*Level // node's index
}
type Level struct {
next *Node
}
type SkipList struct {
hn *Node // header
h int // height
c int // count
}
func New() *SkipList {
return &SkipList{
hn: NewNode(MAX_L, 0), // head node doesn't count
h: 1,
c: 0,
}
}
func NewNode(level, val int) *Node {
node := new(Node)
node.v = val
node.ls = make([]*Level, level)
for i := 0; i < len(node.ls); i++ {
node.ls[i] = new(Level)
}
return node
}The p here is the node promotion probability,

And MaxLevel is the highest level of the SkipList. Both of these two numbers can be set based on needs. We can infer the height of the SkipList from above.
If inferring backward, we can see that this SkipList can contain 2³² elements in maximum, that is, n = 2³².
Operation
Now to implement the three main methods of insert, query, and delete after defining the data structure.
First, have a look at the insert algorithm, also the most complicated part, in which you need to build the relevant index levels for each newly inserted element.
The above is the pseudo-code of the algorithm for building levels, the key is quasi-random.
To explain it in code from my understanding is
/**
get a random level, the odds is
1/2 = 1
1/4 = 2
1/8 = 3
...
1/2 + 1/4 + 1/8 ... + 1/n
*/
func (sl *SkipList) randomL() int {
l := 1
r := rand.New(rand.NewSource(time.Now().UnixNano()))
for r.Float64() < P && l < MAX_L {
l++
}
return l
}
The ground level is 1, and p == 0.5, so the probability of a newly added element building an n-level index is
odds = ½ + ½*½ + ½*½*½ … ½^n
Upon understanding the algorithm for the random calculation of levels, it only takes 2 main steps to complete the inserting.
- Locate the insert position, find the node before the insert position in each level of index element, and record it. For example, to insert an element at index:2, you must know the node of index:1 new_node.next=node1.next;node1.next=new_node.
update := make([]*Node, MAX_L) th := sl.hn for i := sl.h - 1; i >= 0; i-- { // find the right place in each level for th.ls[i].next != nil && th.ls[i].next.v < value { th = th.ls[i].next } // make sure no duplicates if th.ls[i].next != nil && th.ls[i].next.v == value { return false } update[i] = th }
- Build new levels, if needed. Otherwise, insert new nodes directly after each level’s node.
// get the level for the new item level := sl.randomL() node := NewNode(level, value) if level > sl.h { sl.h = level } for i := 0; i < level; i++ { // concat new node of the upper level to the head node if update[i] == nil { sl.hn.ls[i].next = node continue } // insert node node.ls[i].next = update[i].ls[i].next update[i].ls[i].next = node }
Now about the much easier query method: Just search the element from the top level down until you find it. Sometimes you can’t find it even at the bottom level.
th := sl.hn
// search for the top level
for i := sl.h - 1; i >= 0; i-- {
for th.ls[i].next != nil && th.ls[i].next.v <= value {
th = th.ls[i].next
}
// if no match, then search the next level
if th.v == value {
node = th
break
}
}
if node == nil {
return nil, false
}
Finally, the delete function, which almost reverses the insert process.
- Try to find the node, and record the position of the node index in each level.
- Delete the node, including the corresponding node in each index level.
- Remove the empty levels, if any.
In addition to these 3 main methods, we can also add some other methods, such as IsEmpty, Count, etc.
For complete code and tests, please check git.
The end
Some may think that doing the algorithm will sometimes cause some brain cells to “die from overwork”, but I think those cells that can “survive” are the best. Just kidding!
Though there’s probably no obvious practical effect on daily work since most of the algorithm structures have been encapsulated in the library for direct use, I still believe the algorithm practice can help improve the overall coding capability. At least, one piece a week keeps me on track.
Reference
https://en.wikipedia.org/wiki/Skip_list
Note: The post is authorized by original author to republish on our site. Original author is Stefanie Lai who is currently a Spotify engineer and lives in Stockholm, original post is published here.
