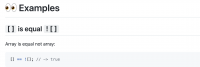
You may be familiar with integer overflow, but what you may not be familiar with is how gcc handles signed integer overflow.
First let's look at the standard, for unsigned integer, the standard says :
A computation involving unsigned operands can never overflow, because a result that cannot be represented by the resulting unsigned integer type is reduced modulo the number that is one greater than the largest value that can be represented by the resulting type.
In other words, unsigned integer overflow will be wrapped so that it will be still in the range of an unsigned integer.
For signed integer, the standard says it's an undefined behavior:
If an exceptional condition occurs during the evaluation of an expression (that is, if the result is not mathematically defined or not in the range of representable values for its type), the behavior is undefined.
In fact(with 2's complement), if there is an overflow, the result will be a negative integer, it will beyond the range of positive integer. On wikipedia:
Most computers distinguish between two kinds of overflow conditions. A carry occurs when the result of an addition or subtraction, considering the operands and result as unsigned numbers, does not fit in the result. Therefore, it is useful to check the carry flag after adding or subtracting numbers that are interpreted as unsigned values. An overflow proper occurs when the result does not have the sign that one would predict from the signs of the operands (e.g. a negative result when adding two positive numbers). Therefore, it is useful to check the overflow flag after adding or subtracting numbers that are represented in two's complement form (i.e. they are considered signed numbers).
Because of the undefined behavior, so gcc makes a surprising optimization.
C:
-
#include <limits.h>
-
#include <stdio.h>
-
-
int wrap(int a) {
-
return (a + 1> a);
-
}
-
-
int main(void) {
-
}
It's easy to understand, gcc may generate the following codes
00000000004004f0 :
4004f0: b8 01 00 00 00 mov $0x1,%eax
4004f5: c3 retq
since gcc assumes signed integer will never overflow, so a+1>a will always be true, it will return 1 diectly. This conforms to the standard, but don't conform to our expectation, we expect wrap() can check whether it overflows or not.
gcc introduces some related command line options: -fwrapv,-fstrict-overflow/-fno-strict-overflow,-Wstrict-overflow.
-fstrict-overflow tells compiler signed integer overflow is undefined, you can assume it will not happen so that you can do further optimization. -fwrapv tells the compiler that signed integer overflow is well defined, it is wrap. gcc document says:
Using -fwrapv means that integer signed overflow is fully defined: it wraps. When -fwrapv is used, there is no difference between -fstrict-overflow and -fno-strict-overflow for integers. With -fwrapv certain types of overflow are permitted. For example, if the compiler gets an overflow when doing arithmetic on constants, the overflowed value can still be used with fwrapv, but not otherwise.
When we add -fno-strict-overflow, the generated codes
00000000004004f0 :
4004f0: 8d 47 01 lea 0x1(%rdi),%eax
4004f3: 39 f8 cmp %edi,%eax
4004f5: 0f 9f c0 setg %al
4004f8: 0f b6 c0 movzbl %al,%eax
4004fb: c3 retq
For machines using 2's complement,-fwrapv and -fno-strict-overflow has little difference.
There was a related bug in Linux kernal, some Linux expert fixed this but, he said:
It looks like 'fwrapv' generates more temporaries (possibly for the code that treies to enforce the exact twos-complement behavior) that then all get optimized back out again. The differences seem to be in the temporary variable numbers etc, not in the actual code.
So fwrapv really _is_ different from fno-strict-pverflow, and disturbs the code generation more.
IOW, I'm convinced we should never use fwrapv. It's clearly a buggy piece of sh*t, as shown by our 4.1.x experiences. We should use -fno-strict-overflow.
So when compiling Linux kernal, we will use -fno-strict-overflow.